Factorizacion de polinomios

¿Que es la factorización?

La factorizacion, es la representación de una expresión algebraica como producto. cada elemento del producto recibe el nombre de factor.

La factorizacion es el proceso inverso de la multiplicación de factores.

El estudio de factorización requiere de habilidades y conocimientos algebraicos básicos.

En esta ocasión , veremos cinco casos de factorización.

Máximo común divisor de polinomios

Para encontrar el máximo común denominador (m.c.d.) de dos o mas términos, debemos encontrar el m.c.d. de los coeficientes y multiplicarlos por la mínima potencia de las variables que aparecen en cada monomio.

Ejemplo: Encontrar el m.d.c. de  

Solución: 

Monomios	Factores de los coeficientes	Factores de las literales
	4.5
	4.4

Los factores son    4   y    

El máximo común divisor de la expresión es: 

El m.c.d. nos sirve para los polinomios como producto de su máximo factor común y otro mas sencillo que el original, el ejemplo anterior quedará factorizado de la siguiente manera:

1. Factorizacion de un monomio a partir de un polinomio.

Se realiza siguiendo estos tres sencillos pasos.

1.-Determinar el m.c.d. (máximo común divisor) de todos los términos del polinomio.

2.-Escribir todos los términos como el producto del m.c.d. y sus otros factores 

3.-Utilizar la propiedad distributiva para factorizar el m.c.d.

Ejemplo 1: Factorizar     15x - 20

Solución: 

El m.c.d. de cada termino respectivamente es:

15x = 5 * 3 x             20= 5 * 4

El m.c.d. es 5 al factorizar el MCD queda: 15x - 20 = (5) (3x - 4)

Ejemplo 2: Factorizar     

Solucion:

El m.c.d. de cada termino respectivamente es:

             

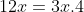
El m.c.d. es 3x al factorizar el MCD queda:   

Triangulo de Pascal

Las matemáticas y el triangulo de pascal

Como podemos observar cuando la potencia del binomio aumenta, el numero de términos incrementa. Si observas los números de términos,siempre es un grado mayor a la potencia a la que se encuentra elevado el binomio.

Hay problemas en matemáticas financieras, como es el calculo de interés compuesto, ya sea para un préstamo o para un monto en el que se desea saber cuanto vamos a pagar o recibir después de un tiempo y la expresión que se utiliza para este tipo de problema es M=C(1+i)^n, para determinar el resultado de multiplicar n veces un binomio nos podemos auxiliar del triangulo de pascal, que es una representación de los coeficientes binomiales en forma triangular, que se llama así en honor al francés Blaise Pascal quien fue un filosofo, físico y matemático.

Observar en la figura anterior que cada numero interior es la suma de los que están colocados directamente arriba de el.

Analicemos algunos binomios:







Los coeficientes de cada uno de los términos corresponden al triangulo de pascal. Analizando las potencias de los términos del binomio, puedes observar que el resultado del primer binomio a la potencia cero es (1); para un binomio elevado a la potencia 1, corresponde a los mismos términos del binomio. a partir del binomio 2, el primer termino tiene la misma potencia que el binomio, el segundo termino contiene a ambos términos, el primer termino disminuido en un grado y el segundo termino elevado a la primera potencia y al tercer termino tiene la misma potencia que el primero,este desarrollo se puede observar en cada uno de los términos, de tal manera que el primer termino disminuye en la potencia una unidad y el segundo aumenta en una unidad, hasta la potencia del binomio, ademas el numero de términos siempre es n+1 donde n es el grado del polinomio.

Ejemplo: a continuación Desarrollaremos  utilizando el triangulo de pascal.

Solución:

procedimiento:


simplificando


Nota: Podrás observar que los coeficientes corresponden al triangulo de pascal

Productos notables

¿Que son los productos notables?

A continuación detallaremos que algunos conceptos de productos notables.

• Tanto en la multiplicación aritmética como algebraica se sigue un algoritmo, sin embargo, existen productos algebraicos que pueden calcularse a través de normas establecidas, estos productos reciben el nombre de productos notables.

• Normas que se establecen para resolver algunas multiplicaciones, sin verificar la multiplicación.

Existen cuatro casos principales de productos notables, las cuales analizaremos en este contenido.


1.- Cuadrado de suma y diferencia de binomio

El producto de un binomio por si mismo recibe el nombre de cuadrado del binomio . el desarrollo de un cuadrado de binomio siempre tiene la misma estructura.

( a + b )^2 = ( a + b ) ( a + b )

si realizamos el producto termino a termino, obtenemos.

 ${\displaystyle =a\cdot a+b\cdot a+a\cdot b+b\cdot b}$ ${\displaystyle =a^{2}+2\cdot a\cdot b+b^{2}}$


Esto quiere decir que:

Por lo tanto:

El cuadrado de la suma de dos números, es el cuadrado del primer termino, mas el doble producto del primer termino por el segundo termino, mas el cuadrado del segundo termino.


La expresión siguiente se conoce como trinomio cuadrado perfecto.

El cuadrado del binomio como otros productos notables, tiene una representación geométrica en el plano. consiste en determinar el área del cuadrado de lado a+b.

Para determinar el área del cuadrado de la figura 1.0, multiplicamos las longitudes de sus lados, es decir (a + b) (a + b), o lo que es lo mismo sumar las áreas de los rectángulos internos como se muestra en la figura 1.1



Ejemplo:Desarrollar el binomio    

Solución:



Cuando el binomio es una diferencia, se conoce como el cuadrado de la diferencia de dos números, es decir:

Ejemplo:

${\displaystyle (2x-3y)^{2}=(2x)^{2}-2(2x)(3y)+(3y)^{2}\,}$

Simplificando:

${\displaystyle (2x-3y)^{2}=4x^{2}-12xy+9y^{2}\,}$

2.- Binomios con un termino común 

Corresponde a la multiplicación de binomios donde el primer termino es común para ambos binomios, por ejemplo

 ${\displaystyle x\cdot x+a\cdot x+x\cdot b+a\cdot b=}$ ${\displaystyle x^{2}+(a+b)x+a\cdot b}$

Esto significa que el producto de dos binomios con un termino en común, es.

El binomio con un termino común, es el cuadrado del termino común, mas la suma de los dos términos distintos multiplicados por el termino común,mas el producto de los términos distintos.

     Ejemplo:

1.- 

${\displaystyle (2y-1)(2y-3)=(2y)^{2}+(-1-3)(2y)+((-1)(-3))=4y^{2}-8y+3}$2.- 

3.- Productos de dos binomios conjugados 

Se llaman binomios conjugados al producto de la suma de dos números por su diferencia, se caracteriza por ser un producto de dos binomios con términos iguales, que difieren en que un binomio tiene signo positivo y el otro negativo, por ejemplo.

El producto de dos binomios conjugados, es el cuadrado del primer termino, menos el cuadrado del segundo termino.

Algunos ejemplos del producto de dos binomios conjugados son:

1.- 

2.- 

4.- Binomio al cubo.

El desarrollo del cubo del binomio (a + b) se puede obtener, multiplicando este por su cuadrado.

La suma del binomio al cubo es, el cubo del primer termino, mas el triple producto del cuadrado del primer termino por el segundo, mas el triple producto del primer termino por el cuadrado del segundo termino, mas el cubo del segundo termino.

Binomio al cubo